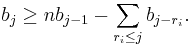Golod–Shafarevich theorem

In mathematics, the Golod–Shafarevich theorem was proved in 1964 by two Russian mathematicians, Evgeny Golod and Igor Shafarevich. It is a result in non-commutative homological algebra which has consequences in various branches of algebra.

The inequality

Let A = K<x₁, ..., x_n> be the free algebra over a field K in n = d + 1 non-commuting variables x_i.

Let J be the 2-sided ideal of A generated by homogeneous elements f_j of A of degree d_j with

2 ≤ d₁ ≤ d₂ ≤ ...

where d_j tends to infinity. Let r_i be the number of d_j equal to i.

Let B=A/J, a graded algebra. Let b_j = dim B_j.

The fundamental inequality of Golod and Shafarevich states that

$b_j\ge nb_{j-1} -\sum_{r_i\le j} b_{j-r_i}.$

As a consequence:

B is infinite-dimensional if r_i ≤ d²/4 for all i

if B is finite-dimensional, then r_i > d²/4 for some i.

Applications

This result has important applications in combinatorial group theory:

If G is a nontrivial finite p-group, then r > d²/4 where d = dim H¹(G,Z/pZ) and r = dim H²(G,Z/pZ) (the mod p cohomology groups of G). In particular if G is a finite p-group with minimal number of generators d and has r relators in a given presentation, then r > d²/4.

For each prime p, there is an infinite group G generated by three elements in which each element has order a power of p. The group G provides a counterexample to the generalised Burnside conjecture: it is a finitely generated infinite torsion group, although there is no uniform bound on the order of its elements.

In class field theory, the class field tower of a number field K is created by iterating the Hilbert class field construction. Another consequence of the construction is that such towers may be infinite (in other words, do not always terminate in a field equal to its Hilbert class field).

References

Golod, E.S; Shafarevich, I.R. (1964), "On the class field tower", Izv. Akad. Nauk SSSSR 28: 261–272 (in Russian) MR 0161852
Golod, E.S (1964), "On nil-algebras and finitely approximable p-groups.", Izv. Akad. Nauk SSSSR 28: 273–276 (in Russian) MR 0161878
Herstein, I.N. (1968), "Noncommutative rings," Carus Mathematical Monographs, MAA. ISBN 0-88385-039-7. See Chapter 8.
Johnson, D.L. (1980). "Topics in the Theory of Group Presentations" (1st ed.). Cambridge University Press. ISBN 0-521-23108-6. See chapter VI.
Roquette, P. (1967), On class field towers,pages 231–249 in Algebraic number theory, Proceedings of the instructional conference held at the University of Sussex, Brighton, September 1–17 , 1965. Edited by J. W. S. Cassels and A. Fröhlich. Reprint of the 1967 original. Academic Press, London, 1986. xviii+366 pp. ISBN 0-12-163251-2
Serre, J.-P. (2002), "Galois Cohomology," Springer-Verlag. ISBN 3-540-42192-0. See Appendix 2. (Translation of Cohomologie Galoisienne, Lecture Notes in Mathematics 5, 1973.)